Problema de la semana 2021-37

Semana del 13 al 19 de septiembre de 2021

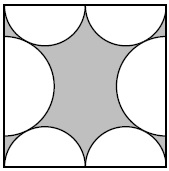
En la figura, las semicircunferencias son tangentes entre sí. Si el área del cuadrado vale A y la suma de las áreas de las 6 semicircunferencias vale B. ¿Cuánto es $\frac{B}{A}$ ?

Solución

Digamos que el radio de una de las semicircunferencias chicas es $r_1$ y el radio de una de las semicircunferencias grandes es $r_2$ . Trazando un segmento desde el centro de una semircircunferencia grande hasta el centro de una de las semicircunferencias tangente a ella, obtenemos un triángulo rectángulo con un cateto igual a $r_1$ , el otro cateto igual a $\frac{\sqrt{A}}{2}$ y la hipotenusa igual a $r_1+r_2$ . Aplicamos el teorema de pitágoras.