Problema de la semana 2021-16

Calcule el valor de la siguiente suma infinita:

$S=\frac{1}{2}+\frac{2}{2^2}+\frac{3}{2^3}+\frac{4}{2^4}+\frac{5}{2^5}+\cdots$

Recordemos primero la fórmula para la suma de una progresión geométrica:

$S_g=1+r+r^2+r^3+\dots+r^n=\frac{1-r^n}{1-r}$

Si $r<1$ y $n\rightarrow \infty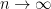$ , entonces $S_g=\frac{1}{1-r}$ .

Vemos ahora que la suma se puede escribir de la siguiente manera

$S=\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^2}+\frac{1}{2^3}+\frac{1}{2^3}+\frac{1}{2^3}+\dots$

Vamos a definir las siguientes sumas.

$S_1=\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\frac{1}{2^4}+\dots$

$S_2=\frac{1}{2^2}+\frac{1}{2^3}+\frac{1}{2^4}+\frac{1}{2^5}+\dots=\frac{1}{2}S_1$

$S_3=\frac{1}{2^3}+\frac{1}{2^4}+\frac{1}{2^5}+\frac{1}{2^6}+\dots=\frac{1}{4}S_1$

Y así sucesivamente para $S_4,S_5,S_6,\dots$ .

Podemos entonces escribir $S$ de la siguiente manera:

$S=S_1 + S_2 + S_3 +\dots$

$S=S_1+\frac{1}{2}S_1+\frac{1}{2^2}S_1+\frac{1}{2^3}S_1+\dots$

$S=S_1(1+\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\frac{1}{2^4}+\dots)$

$S=S_1(1+S_1)$

Usando la fórmula de la progresión aritmética, calculamos $S_1=\frac{1}{2}(\frac{1}{1-\frac{1}{2}})=1$

Por consiguiente, tenemos que $S=1(1+1)=2$ .