Problema de la semana 2021-14
Semana del 5 al 11 de abril de 2021
Considerando la figura que se muestra a continuación, calcule el valor de x.
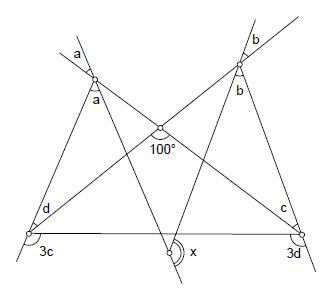
Digamos que el ángulo que está entre d y 3c se llama e, y son suplementarios así que
[1] .
Digamos que el ángulo que está entre c y 3d se llama f, y son suplementarios así que
[2] .
Sumando [1] y [2] resulta
[3]
La suma de los ángulos internos de un triángulo es 180°, así que , lo que implica que
. Conisiderando este último resultado en la ecuación [3], obtenemos que
Vemos que el triángulo de arriba a la izquierda tiene un ángulo que mide d, un ángulo que mide 2a y un ángulo que mide 80°. El triángulo de arriba a la derecha tiene un ángulo que mide c, un ángulo que mide 2b y un ángulo que mide 80°. De aquí obtenemos lo siguiente:
El resultado de sumar las ecuaciones es
Pero sabemos que , así que
Por último, fijándonos en el triángulo pequeño que está abajo en el medio de la figura (donde se marca la x), y recordando que la suma de dos ángulos de un triángulo es igual al tercer ángulo exterior, notamos lo siguiente
El valor de x es 145°.

