Problema de la semana 2021-5

Semana del 31 de enero al 6 de febrero de 2021

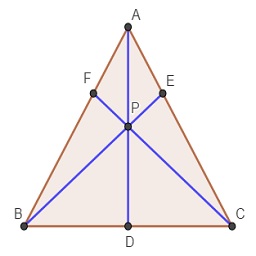
ABC es un triángulo equilátero. D es el punto medio del lado $\overline{BC}$ . Los puntos Ey F dividen a los lados $\overline{AC}$ y $\overline{AB}$ en una razón de 1:2. Los segmentos $\overline{AD}$ , $\overline{BE}$ y $\overline{CF}$ concurren en el punto P. ¿Cuánto vale $\frac{[APE]}{[ABC]}$ ?

Nota: usamos la notación $[XYZ]$ para referirnos al área del polígono formado por los vértices $XYZ$ .

Solución

Observamos primeramente que $\triangle APE \cong \triangle APF$ , $\triangle FPB \cong \triangle EPC$ y que $\triangle PDC \cong \triangle PDB$ .

Digamos que $[APE]=S$ y $[CPD]=T$ .

Trazamos el segmento perpendicular que va de P al lado AC. Vemos que este segmento es una altura para el triángulo APE y también para el triángulo EPC. Como estos dos triángulos tienen la misma altura, la razón de sus áreas es igual a la razón de sus bases, es decir,

$\frac{[APE]}{[EPC]}=\frac{AE}{EC}=\frac{1}{2}$

Dicho de otra forma, $[EPC]=2[APE]=2S$

Siguiendo el mismo razonamiento, observamos que

$[EBC]=2[ABE]$
$2T+2S=2(4S)$
$T=3S$

Vemos que $\triangle ABC$ está formado por seis triángulos internos cuyas áreas suman $S+S+2S+2S+T+T=12S$

Por último, $\frac{[APE]}{[ABC]}=\frac{S}{12S}=\frac{1}{12}$

Problema de la semana 2021-5

Semana del 31 de enero al 6 de febrero de 2021

Solución

Recibe las noticias

Redes sociales

Portales internos